library(tidyverse)
library(hrbrthemes)
set.seed(3756)Simulation and Twitter riddles
Hi everyone!
Earlier today I stumbled upon this tweet by Sean J. Taylor:
Without doing the math or looking it up, approximately how many coin flips do you need to observe in order to be 95% confident you know Prob(Heads) to within +/- 1%?
— Sean J. Taylor (@seanjtaylor) April 22, 2021
…and I asked myself:
Can we answer this using simulation?
The answer is that yes, yes we can! Let’s see how we can do that using R (of course). Looks like this is now primarily a statistical simulation blog, but hey…
Let’s start by loading some packages and setting an RNG seed for reproducibility:
Then, we define a function that we will use to replicate this experiment:
simfun <- function(i, .prob, .diff = 0.02, .N = 100000, .alpha = 0.05) {
draw <- rbinom(n = .N, size = 1, prob = .prob)
df <- tibble(
n = seq(.N),
x = cumsum(draw),
mean = x / n,
lower = (1 + (n - x + 1) / (x * qf(.alpha / 2, 2 * x, 2 * (n - x + 1))))^(-1),
upper = (1 + (n - x) / ((x + 1) * qf(1 - .alpha / 2, 2 * (x + 1), 2 * (n - x))))^(-1),
width = upper - lower
)
out <- tibble(i = i, prob = .prob, diff = .diff, y = min(which(df$width <= .diff)))
return(out)
}This function:
Repeates the experiment for 1 to 100,000 (
.N) draws from a binomial distribution (e.g. our coin toss), with success probability.prob;Estimates the cumulative proportion of heads (our ones) across all number of draws;
Estimates confidence intervals using the exact formula;
Calculates the width of the confidence interval. For a +/- 1% precision, that corresponds to a width of 2% (or 0.02, depending on the scale being used);
Finally, returns the first number of draws where the width is 0.02 (or less). This will tell us how many draws we needed to draw to get a confidence interval that is narrow enough for our purpose.
Then, we run the experiment B = 200 times, with different values of .prob (as we want to show the required sample sizes over different success probabilities):
B <- 200
results <- map_dfr(.x = seq(B), .f = function(j) {
simfun(i = j, .prob = runif(1))
})Let’s plot the results (using a LOESS smoother) versus the success probability:
ggplot(results, aes(x = prob, y = y)) +
geom_point() +
geom_smooth(method = "loess", size = 1, color = "#575FCF") +
scale_x_continuous(labels = scales::percent) +
scale_y_continuous(labels = scales::comma) +
coord_cartesian(xlim = c(0, 1)) +
theme_ipsum(base_size = 12, base_family = "Inconsolata") +
theme(plot.margin = unit(rep(1, 4), "lines")) +
labs(x = "Success probability", y = "Required sample size")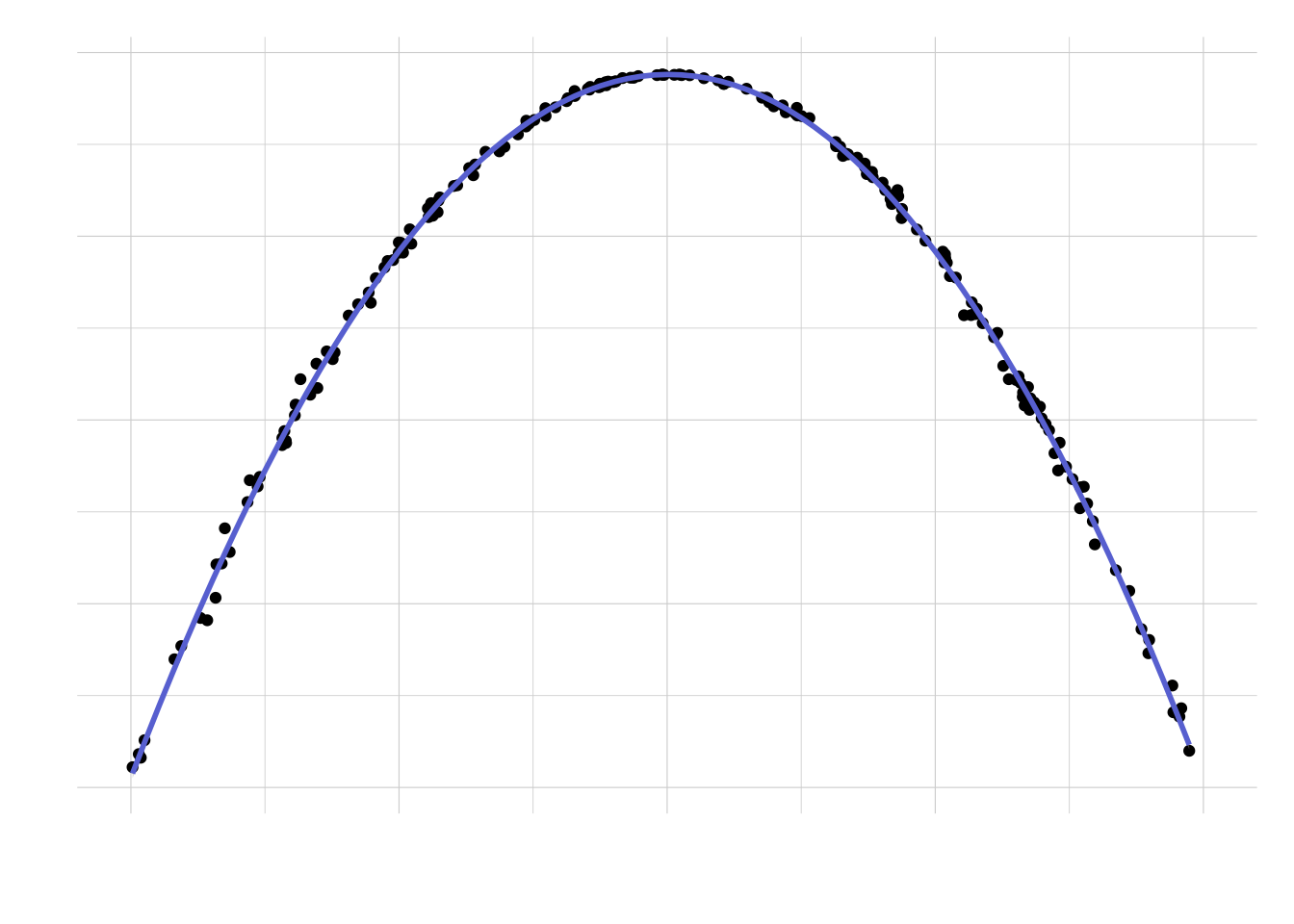
Looks like — as one would expect — the largest sample size required is for a success probability of 50%. What is the solution to the riddle then? As any statistician would confirm, it depends: if the coin is fair, then we would need approximately 10,000 tosses. Otherwise, the required sample size can be much smaller, even a tenth. Cool!
Finally, let’s repeat the experiment for a precision of +/- 3%:
results_3p <- map_dfr(.x = seq(B), .f = function(j) {
simfun(i = j, .diff = 0.06, .prob = runif(1))
})Comparing with the previous results (code to produce the plot omitted for simplicity):
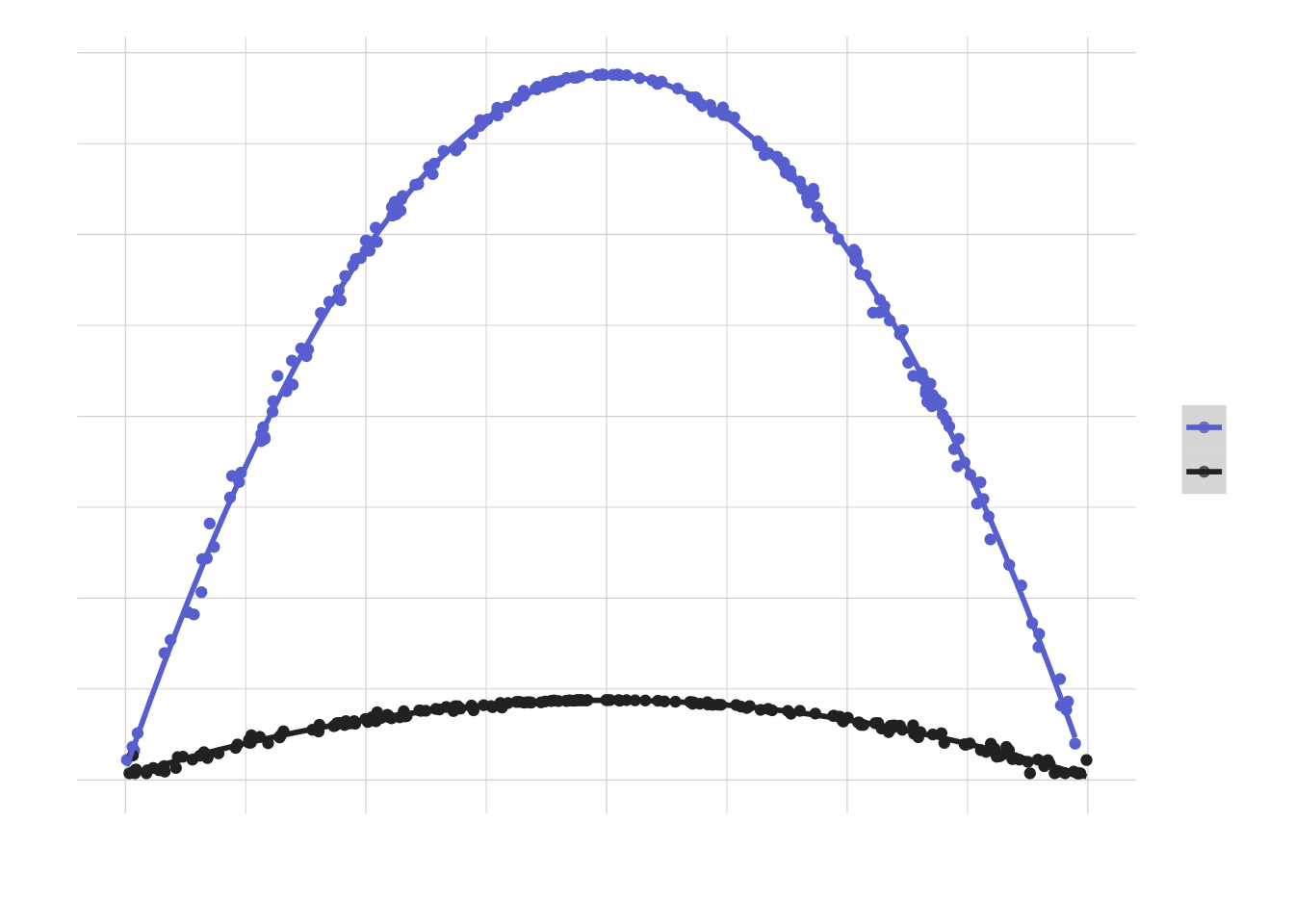
For a required precision of +/- 3% the sample size that we would need is much smaller, but the shape of the curve (i.e. versus the success probability) remains the same.
Finally, the elephant in the room: of course we could answer this using our old friend mathematics, or with a bit of Bayesian thinking. But where’s the fun in that? This simulation approach lets us play around with parameters and assumptions (e.g. what would happen if we assume a difference confidence level .alpha?), and it’s quite intuitive too. And yeah, let’s be honest: programming and running the experiment is just much more fun!
As always, please do point out all my errors on Twitter. Cheers!